Current Projects

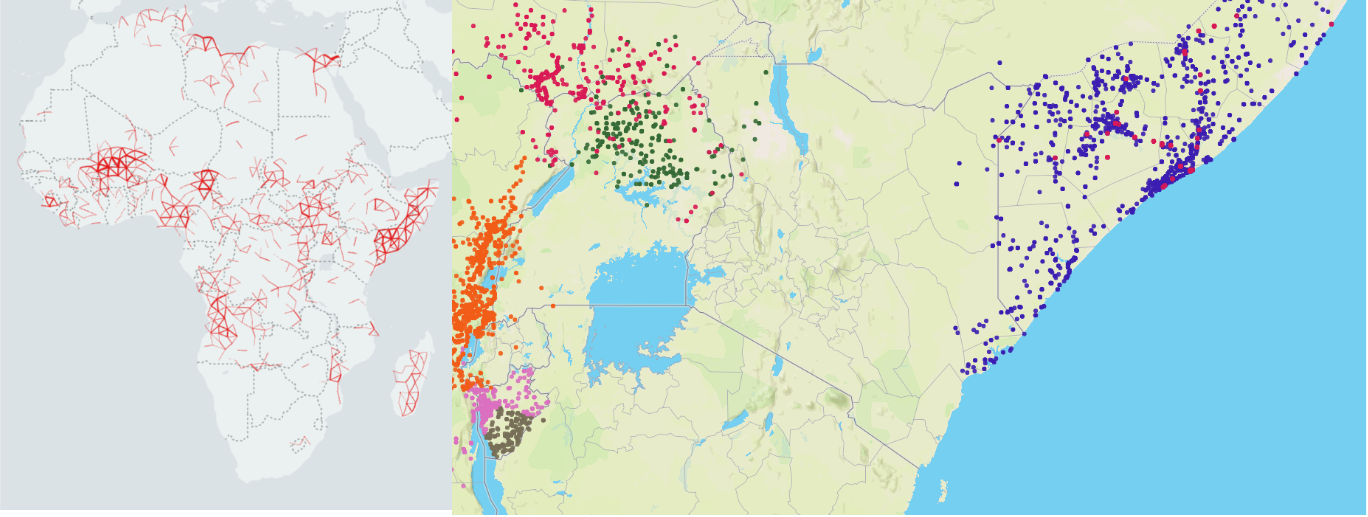
Conflicts, like many social processes, are related events that span multiple scales in time, from the instantaneous to multi-year developments, and in space, from one neighborhood to continents. Yet, there is little systematic work on connecting the multiple scales, formal treatment of causality between events, and measures of uncertainty for how events are related to one another. We develop a method for extracting related chains of events that addresses these limitations with armed conflict. Our method explicitly accounts for an adjustable spatial and temporal scale of interaction for clustering individual events from a detailed data set, the Armed Conflict Event & Location Data Project. With it, we discover a mesoscale ranging from a week to a few months and from tens to a few hundred kilometers, where long-range correlations and nontrivial dynamics relating conflict events emerge. Importantly, clusters in the mesoscale, while extracted only from conflict statistics, are identifiable with causal mechanism cited in field studies. We leverage our technique to identify zones of causal interaction around conflict hotspots that naturally incorporate uncertainties. Thus, we show how a systematic, data-driven procedure extracts social objects for study, providing a scope for scrutinizing and predicting conflict amongst other processes.

The mathematical laws of life manifest scaling regularities such as the relationship between mass and metabolism for the smallest to the largest organisms on Earth. These laws lack essential components representing interaction between organisms while sharing limited resources. Once accounted for, these components can bring significant variation to the predicted demographic laws using just metabolic scaling theory and can give mathematical descriptions for observed ecological phenomena. The oscillations in population number, where spikes in the number of organisms of a specific size propagate from small to large organisms is an example of such a phenomena. Here, we incorporate spatial competition and resource variation in a differential equation model for the population dynamics of sessile organisms. We use analytic and numerical tools to solve the corresponding equations and to characterize the form of instabilities that generate the oscillations, which we use to identify hidden mechanisms that may drive instabilities in ecological systems such as forests. As a result, we may be able to identify the most significant factors that affect the stability of an ecosystem corresponding to resource fluctuations that may become more prominent with climate change.